y²=4xにおいて，dy/dxの値を求める問題です。dy/dxの記号の意味がわからないと，いったいどんな計算をしてよいかわかりませんね。今回は， d/dx，d/dy，dy/dx などの意味から解説していきます。

d/dxは，簡単に言うと， 「文字xで微分する」 操作を表す記号です。同様に，d/dyは，「文字yで微分する」 操作を表す記号となります。

「d」は，微小変化を表す文字で，「dx」は「ほとんど0に近い微小変化するときのx」を表します。したがって，例えば，
(d/dx)(3x)
は，簡単に言うと， 「3xを文字xで微分する」 になります。より詳しく言うと，「xが0に近い微小変化をするときの3xの変化の割合」であり，いずれも値は，
(d/dx)(3x)=3
となりますね。

大事なポイントは，

です。まずは，ここをしっかりとおさえましょう。

次に，dy/dxについて解説しましょう。dy/dxは，簡単に言うと， 「yをxで微分したときの値」 を表します。(d/dx)y も同じ意味を表します。

dy/dxは，厳密には分数ではなく，yをxで微分したときの値です。しかし，微分はそもそも分数式の極限に由来するものなので，dy/dxは計算式で分数と同じように扱うことができます。

前置きが長くなってしまいましたね。dy/dxの意味をつかんだところで，y²=4xの式をもとに，dy/dxの値を求めましょう。

この問題は，与えられた式が「y²=～」の形になっている点が面倒です。仮に，「y=f(x)」の形であれば，両辺をxで微分することにより，「dy/dx=f'(x)」で答えを出すことができます。

このようなときも，まずは「y²=4x」の両辺をxで微分してみましょう。すると，
(d/dx)y²=4×1
と手掛かりが見えてきます。

求めたいのは，dy/dxの値でしたね。そこで，
(d/dx)y²=4
の式において，y²をyで微分し，強引にdy/dxをつくる補正計算をします。

上式では，d/dyによってy²をyで微分しています。しかし，左辺だけyで微分すると等式は成り立ちません。yで微分するとともに，dy/dxによってyをxで微分して補正計算を行っています。このとき，微分の記号を分数式のように見立てると，
(d/dy)×(dy/dx)
となり，ちょうどdyが約分で消えて，もとの(d/dx)が残ることがわかりますね。dy/dxは，このように分数と同じように扱うことができるのです。

式に(dy/dx)をつくることができたら，あとは次のように計算を進めれば，答えが出てきます。

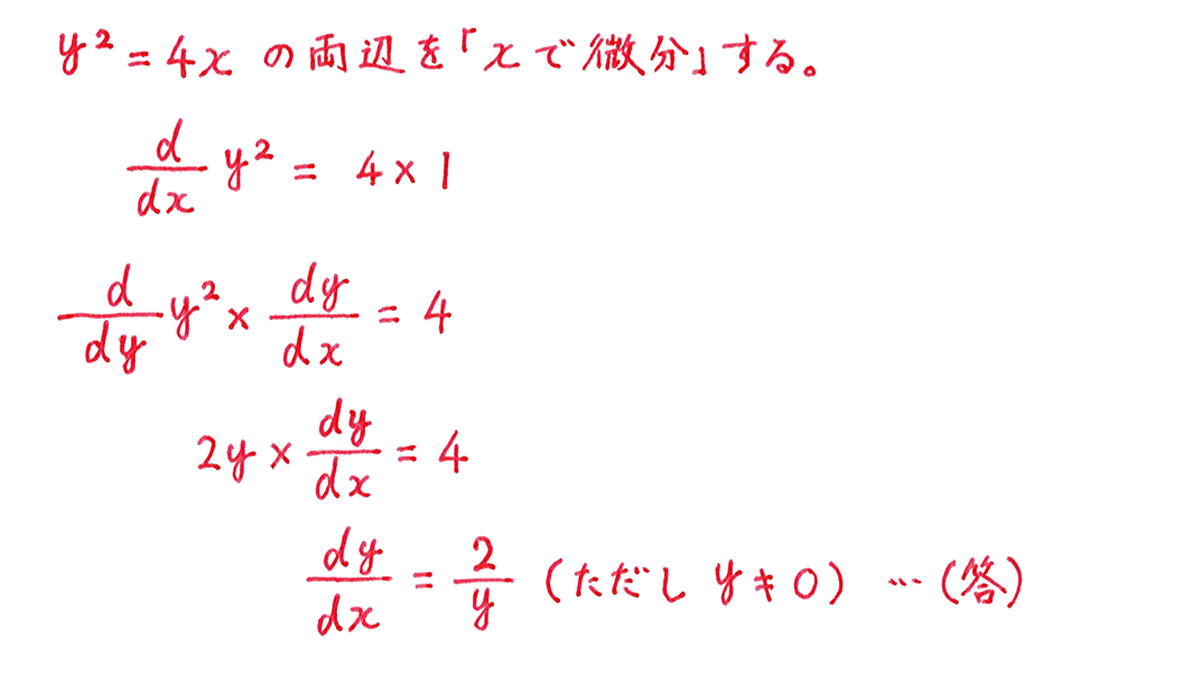
d/dxやdy/dxの意味をより深く理解するには，大学数学の知識も必要となってきます。ここでは，次のポイントをしっかりおさえておくようにしましょう。